Answer:
She should use 91 mL of the 60% solution (rounded to the nearest whole number).
Explanation:
The first step to solve this question is to write the correct equations system. The two variables are :
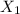 : The amount of high concentration solution (60%) (in mL).
: The amount of high concentration solution (60%) (in mL).
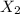 : The amount of low concentration solution (5%) (in mL).
: The amount of low concentration solution (5%) (in mL).
The first equation for the mixing is :
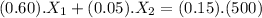 (I)
(I)
Where
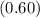 ,
,
 and
and
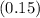 represent the percentages for
represent the percentages for
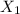 ,
,
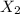 and the final 500 mL of copper-sulfate solution respectively.
and the final 500 mL of copper-sulfate solution respectively.
The second equation is :
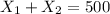 (II)
(II)
The equation (II) represents that the sum from the volumes of high and low concentration solution must be 500 mL.
The final step is to solve this equation system :
From (II) we find that :
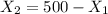 (III)
(III)
If we use (III) in (I) :
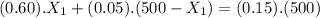
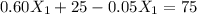
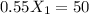
 ≅
≅
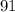
She should use 91 mL of the 60% solution (rounded to the nearest whole number).