Question

The perimeter of a rectangle is 60 meters. What are the possible lengths of any of the rectangle’s sides if its area exceeds 216 square meters? (12, 18) [12, 18)

Answer 1

the possible sides of a rectangle is 12, 18

Explanation:

given:

The perimeter of a rectangle is 60 meters

find:

What are the possible lengths of any of the rectangle’s sides if its area exceeds 216 square meters?

Perimeter (P) = 60 = 2L + 2W ------eq.1

Area (A) = 216 = L x W ---------------eq.2

you can use any of the two equations to to get L or W

say we use the Area = 216 = L x W

L = 216

W

plugin values to eq.1

60 = 2L + 2W

60 = 2( 216 ) + 2W

W

multiply both sides by W

60W = 2(216) + 2W²

60W = 432 + 2W²

rearrange the equation into a quadratic equation:

2W² - 60W + 432 = 0

now, solve for W

- (-60) ±
`√((-60)^2 - 4 * 2 * 432)`

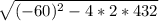
W = --------------------------------------------

2 x 2

W = 60 ± 12

4

W = 12

W = 18

therefore,

the possible sides of a rectangle is 12, 18

Answer 2

Your question is: The perimeter of a rectangle is 60 meters. What are the possible lengths of any of the rectangle’s sides if its area exceeds 216 square meters?

The answer would be (12,18)