Question

30 POINTS AVAILABLE 30 POINTS AVAILABLE

Answer 1

acceleration = 1.3

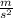
2) acceleration = 26.1

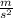
3) acceleration = 2.5

4) Final velocity = 13 m/s

5) Time = 0.7 seconds

Step-by-step explanation:

Answer 2

1) acceleration = 1.3
`(m)/(s^2)`

2) acceleration = 26.1
`(m)/(s^2)`

3) acceleration = 2.5
`(m)/(s^2)`

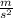
4) Final velocity = 13 m/s

5) Time = 0.7 seconds

Step-by-step explanation:

1) First question:

Acceleration can be calculated based on the formula:

`a=(\Delta v)/(\Delta t) =(15-2.9)/(9) \approx 1.3444\,\,(m)/(s^2)`

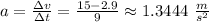
which rounded to one decimal is: 1.3 m/s^2

2) Second question:

Use the formula that relates final and initial velocity with acceleration and distance covered:

`v_f^2-v_i^2=2\,*\,a\,* \,distance\\15^2-4^2=2\,a\,(4)\\209=8 \, a\\a = (209)/(8) \,(m)/(s^2) \\a=26.125\,\,(m)/(s^2)`

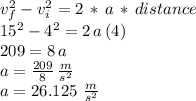
which rounded to one decimal gives:

acceleration = 26.1
`(m)/(s^2)`

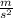
3) Third question :

The marble rolls down 5 meters in 2 seconds, so we use the distance covered formula under constantly accelerated motion:

`distance=v_i\,t+(1)/(2) a\,t^2\\5 = 0 +(1)/(2) a\,(2)^2\\5 = 2 a\\a = 2.5 \,(m)/(s^2)`

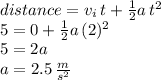
4) Fourth question:

Use the formula

`v_f^2-v_i^2=2\,*\,a\,* \,distance\\v_f^2=7^2+2\,(6)\,(10)\\v_f^2=169\\v_f=√(169) \\v_f=13\,(m)/(s)`

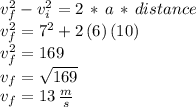
5) Fifth question:

First calculate the acceleration :

`v_f^2-v_i^2=2\,*\,a\, distance\\18.8^2-2.21^2=2\,a\,(60)\\349.03=120\,a\\a=2.908\,(m)/(s^2)`

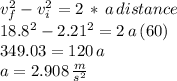
Now we can find the time it takes the car to reach a speed of 4 m/s via the formula:

`v_f-v_i=a\,t\\4-2.1=2.908\,t\\t = 1.9 / 2.908 \,\,s\\t = 0.65337 \,\,s`

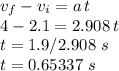
which rounded to one decimal gives:

time = 0.7 seconds