Answer:
f(x, y) = Sin(x*y)
We want the second order taylor expansion around x = 0, y = 0.
This will be:
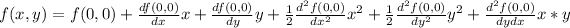
So let's find all the terms:
Remember that:
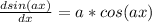
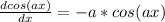
f(0,0) = sin(0*0) = 1.
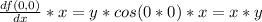

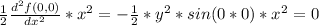
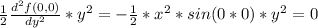

Then we have that the taylor expansion of second order around x = 0 and y = 0 is:
sin(x,y) = x*y + x*y + x*y = 3*x*y