Answer:
3. Last choice: Domain: (-3, 0) U (0, ∞)
4. Last choice: Domain: (-∞, -3) U (-3, ∞), Range: (-∞, 0) U (0, ∞)
Explanation:
3.
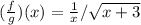
=
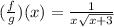
This function will be undefined at x = 0 and x = -3 because the denominator would be equal to 0. This means that the function has vertical asymptotes at x = 0 and x = -3, therefore:
Domain: (-3, 0) U (0, ∞)
*** Remember, x < -3 is not included in the domain because a square root of a negative number does not exist.***
4.
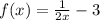
Use "y" instead of f(x), and swap positions of x and y:
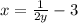
Simplify to isolate for "y":

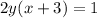
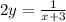
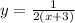
Based on the denominator, the function has a vertical asymptote at x = -3, therefore:
Domain: (-∞, -3) U (-3, ∞)
There is also an EBA asymptote of y = 0 since the denominator has a higher degree than the numerator, so:
Range: (-∞, 0) U (0, ∞)