Answer:
Vertex: (-1,9) is true
Sample Points: (2,4) is not true
Explanation:
Given
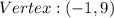

Required
Determine if the vertex and sample points exist for
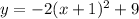
Solving for the vertex:
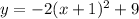
Writing the given equation in the form:
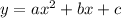
Expand the bracket
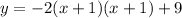
Open Bracket
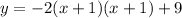
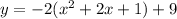
Open bracket
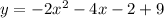

Solve for x using:
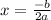
Where
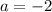 ;
;
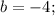
So:
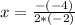

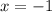
Substitute -1 for x in

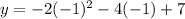
Simplify all brackets
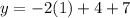
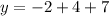
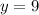
Hence;
The vertex (x,y) is (-1,9)
This is true
Checking sample points:
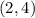
In this case;
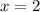 and
and
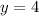
Substitute
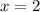 and
and
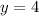 in
in
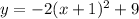
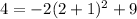
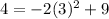
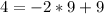
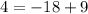

Hence;
This sample points
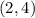 does not exist
does not exist