Question

what is equivalent to (3x^2+2x-8)-(2x^2-4x+7) Answer choices: A)x^2+6x-15 B)x^2+6x-1 C)x^2-2x-15 D)x^2-2x-1

Answer 1

`\boxed{ \bold{ \huge{ \boxed{ \sf{ {x}^(2) + 6x - 15}}}}}`

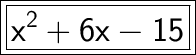
Option A is the correct option.

Explanation:

`\sf{(3 {x}^(2) + 2x - 8) - (2 {x}^(2) - 4x + 7)}`

When there is a ( - ) sign in front of an expression in parentheses , change the sign of each term in the expression

`\longrightarrow{ \sf{3 {x}^(2) + 2x - 8 - 2 {x}^(2) + 4x - 7}}`

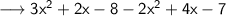
Collect like terms

Only coefficients of like terms can be added or subtracted

`\longrightarrow{ \sf{3 {x}^(2) - 2 {x}^(2) + 2x + 4x - 8 - 7}}`

`\longrightarrow{ \sf{ {x}^(2) + 6x - 8 - 7}}`

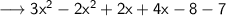
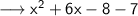
The negative integers are always added but possess the negative ( - ) sign

`\longrightarrow{ \sf{ {x}^(2) + 6x - 15}}`

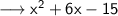
Hope I helped!

Best regards! :D