Answer:
The speed of the submarine is 15.429 miles per hour.
Explanation:
Let suppose that both ships travel at constant velocities. As we know that both travel in opposite directions, it is supposed that cruise ship moves in +x direction, whereas submarine in -x direction. Kinematic equations for each sheep are described below:
Ship
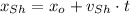
Submarine
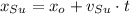
Where:
 - Position of Diego Garcia island, measured in miles.
- Position of Diego Garcia island, measured in miles.
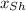 ,
,
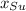 - Current positions of ship and submarine, measured in miles.
- Current positions of ship and submarine, measured in miles.
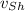 ,
,
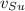 - Velocities of ship and submarine, measured in miles per hour.
- Velocities of ship and submarine, measured in miles per hour.
 - TIme, measured in hours.
- TIme, measured in hours.
If we know that
 ,
,
 and
and
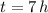 , then:
, then:

We clear now the velocity of submarine:
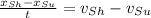


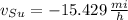
Speed of the submarine is the magnitude of its velocity, which is 15.429 miles per hour.