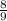Question

Write the sum of the given geometric series as a rational number.

0.8 + 0.08 + 0.008 + 0.0008 + ...
The rational number is:________.
(Simplify your answer. Type an integer or a fraction.)

Answer 1

`(8)/(9)`

Explanation:

Given

Series: 0.8 + 0.08 + 0.008 + 0.0008 + ...

Required

Determine a rational number to represent the series

To do this, we simply get the sum to infinity of the series;

This is done as follows;

`S = (a)/(1 - r)`

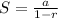
Where a represent the first term

`a = 0.8`

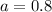
r represent the common ratio

`r = (0.08)/(0.8)`

`r = 0.1`

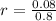
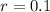
Substitute these values in the above formula

`S = (0.8)/(1 - 0.1)`

`S = (0.8)/(0.9)`

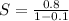
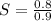
Multiply the numerator and denominator by 10

`S = (8)/(9)`

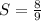
Hence;

The number is
`(8)/(9)`