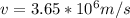Question

What is the speed of an electron with a de Broglie wavelength of 0.20 nm?

Answer 1

`v = 3.65 * 10^6 m/s`

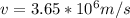
Step-by-step explanation:

Given

de Broglie wavelength = 0.20nm

Required

Determine the speed (v)

The speed is calculated using the following formula;

`L = (h)/(mv)`

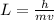
Where

`L = Wavelength = 0.2nm`

`h = Planck's\ constant = 6.63 * 10^(-34)Js`

`m = Mass\ of\ Electron = 9.11 * 10^(-31) kg`

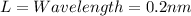
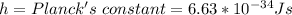
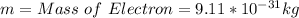
Substitute these values in the above formula

`0.2nm = (6.63 * 10^(-34))/(9.11 * 10^(-31) * v)`

-----------------------------------------------------

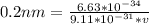
Convert 0.2nm to metre (m)

`0.2nm = 0.2 * 10^(-9)m`

-----------------------------------------------------

`0.2 * 10^(-9) = (6.63 * 10^(-34))/(9.11 * 10^(-31) * v)`

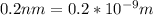
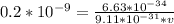
Multiply both sides by v

`v * 0.2 * 10^(-9) = (6.63 * 10^(-34))/(9.11 * 10^(-31) * v) * v`

`v * 0.2 * 10^(-9) = (6.63 * 10^(-34))/(9.11 * 10^(-31) )`

`v * 0.2 * 10^(-9) = (0.73 * 10^(-34))/(10^(-31) )`

`v * 0.2 * 10^(-9) = 0.73 * 10^(-34) * 10^(31)`

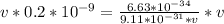
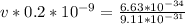
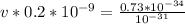
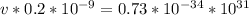
Apply law of indices

`v * 0.2 * 10^(-9) = 0.73 * 10^(-34 + 31)`

`v * 0.2 * 10^(-9) = 0.73 * 10^(-3)`

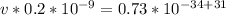
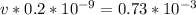
Divide both sides by
`0.2 * 10^(-9)m`

`v = (0.73 * 10^(-3) )/( 0.2 * 10^(-9) )`

`v = (3.65 * 10^(-3) )/(10^(-9) )`

`v = (3.65 * 10^(-3) )/(10^(-9) )`

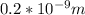
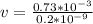
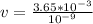
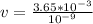
Apply law of indices

`v = 3.65 * 10^(-3) * 10^9`

`v = 3.65 * 10^(-3+9)`

`v = 3.65 * 10^6`

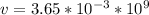
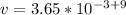
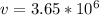
Hence;

The velocity is

`v = 3.65 * 10^6 m/s`