Answer:
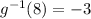
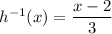
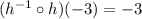 .
.
Explanation:
Given: The one-to-one functions g and h are defined as follows.
g=((-5, 2),( -3, 8), (-1, - 8), (8, 9)) [here each x= input values , y= output values in (x,y)]
h(x)=3x+2
To find:
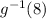
As for 8 is a image of -3 ( from point ( -3, 8)).
So,
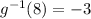
To find :
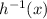
Let
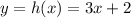 (i)
(i)
Then,
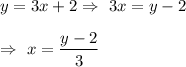
Switch
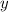 with
with
 and
and
 with
with
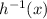 , we get
, we get
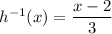 (ii)
(ii)
To find :
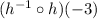
Consider
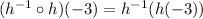
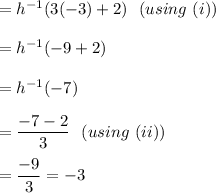
So,
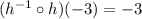 .
.