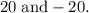Question

Find the absolute maximum and minimum values of f(x,y)=xy−4x in the region bounded by the x-axis and the parabola y=16−x2.

Answer 1

The absolute maximum and minimum is
`20\; \text{and} -20.`

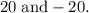
Explanation:

We first check the critical points on the interior of the domain using the

first derivative test.

`f_x=y-4=0`

`f_y=x=0`

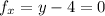
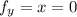
The only solution to this system of equations is the point (0, 4), which lies in the domain.

`f_(xx)=0, \;f_(yy)=0\; \text{and}\; f_(xy)=-1`

`\Rightarrow f_(xx)f_(yy)-f_(xy)=o-1=-1<0`

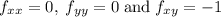
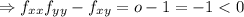
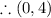`\therefore (0,4)` is a saddle point.

Boundary points -
`(4,0), (-4,0), (0,16)`

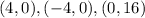
Along boundary
`y=16-x^2`

`f=x(16-x^2)-4x`

`=16x-x^3-4x`

`\Rightarrow f^'=16-3x^2-4=0`

`\Rightarrow 3x^2=12`

`\Rightarrow x=\pm2,\;\;y=14`

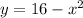
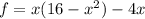
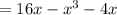
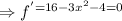
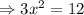
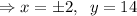
Values of f(x) at these points.

`\begin{array}{}(4,0)=-16\\(-4,0)=16\\(0,16)=0\\(2,14)=20\\(-2,14)=-20\end{array}`

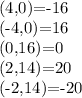
Therefore, the absolute maximum and minimum is
`20\; \text{and} -20.`