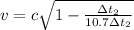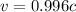Question

How fast should your spacecraft travel so that clocks on board will advance 10.7 times slower than clocks on Earth?

Answer 1

The value is
`v  =  0.996c`

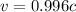
Step-by-step explanation:

From the question we are that

The number by which the clock on the spacecraft should be slower than that on the earth is
`N  =  10.7`

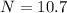
Generally from the time dilation relation given by Albert Einstein we have that

`\Delta t _1  =  \frac{ \Delta t_2 }{ \sqrt{1 -  (v^2)/(c^2 ) } }`

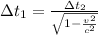
Here
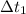`\Delta t _1` is the time on earth

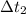`\Delta t _2` is the time on the spacecraft

v is the speed of the spacecraft

c is the speed of light with value
`c=  3.0*10^(8) \  m/s`

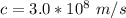
So

`(v^2 )/(c^2)  =  1 -  (\Delta t_2 )/(\Delta t_1)`

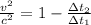
Given that

`\Delta t_1 =  N \Delta t_2`

`\Delta t_1 =  10.7 \Delta t_2`

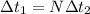
So

`v =  c  \sqrt{ 1 - ( \Delta t_2 )/(10.7 \Delta t_2) }`

`v  =  0.996c`