Question

Let A be the bounded region enclosed by the graphs of f(x)=x, g(x)=x3 . Find the volume of the solid obtained by rotating the region A about the line x+2=0.

Answer 1

Given :

A be the bounded region enclosed by the graphs of
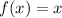`f(x)=x` and
`g(x)=x^3` .

To Find :

The volume of the solid obtained by rotating the region A about the line x+2=0 .

Solution :

Point of intersection of f(x) and g(x) is 0 and 1 .

Volume of solid is given by :

`V=2\pi\int\limits^a_b {(x+p)(f(x)-g(x))} \, dx`

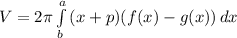
Here , a and b is point of intersection and a = 1 and b = 0 .

Putting all given values in above equation , we get :

`V=2\pi\int\limits^1_0 {(x+2)(x-x^3)} \, dx\\\\V=2\pi\int\limits^1_0(x^2-x^4+2x-2x^3)dx\\\\V=2\pi((x^3)/(3)-(x^5)/(5)+2((x^2)/(2))-2((x^4)/(4)))_0^1\\\\V=2\pi[((1^3)/(3)-(1^5)/(5)+2((1^2)/(2))-2((1^4)/(4)))-((0^3)/(3)-(0^5)/(5)+2((0^2)/(2))-2((0^4)/(4)))]\\\\V=2* \pi *({(1)/(3)-(1)/(5)+1-(1)/(2))\\V=3.96\ units^2`

Therefore , the volume of the solid obtained is
`3.96 \ units^2` .

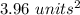Hence , this is the required solution .