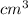Answer:
113.1
Explanation:
The equation to find the volume of a cylinder is:
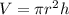
V = volume
r = radius
h = height
The radius of the cylinder is 3 in, and the height of the cylinder is 2 in. Plug these into the equation:
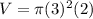
Solve (use calculator):
V =
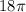 or 56.55
or 56.55
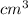
To find the volume of the half sphere use this equation:
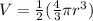
The radius of the circle is 3 in, plug this into the equation:
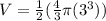
Solve (use calculator):
V =
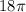 or 56.55
or 56.55
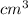
To find the volume of the entire shape just add the separate volumes together:
V( of cylinder) + V( of sphere) = Total volume
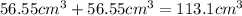
Or, you could rewrite this as 36

So, the answer is that the volume of the composite solid is 113.1