Question

A 15.0 L tank is filled with helium to a pressure of 2.00 * 102 atm. How many balloons (each 2.00 L) can be inflated to a pressure of 1.00 atm, assuming that the temperature remains constant and that the tank cannot be emptied below 1.00 atm?

Answer 1

1493 balloons.

Step-by-step explanation:

Hello,

In this case, we first compute the total moles by temperature by using the ideal gas equation as shown below:

`n_(tot)=(PV)/(RT)=(200atm*15.0L)/(0.082(atm*L)/(mol*K)*T)=36585.4mol/T`

Moreover, since the tank cannot be emptied, we compute the moles that are not transferred:

`n_(not\ transferred)=(1.00atm*15.0L)/(0.082(atm*L)/(mol*K)*T)=182.93mol/T`

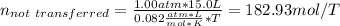
Now, we compute the moles that are actually transferred:

`n_(transferred)=36585.4mol/T-182.93mol/T=36402.5mol/T`

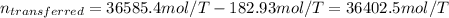
Next, since each balloon is filled up to 1.00 atm within a volume of 2.00 L, the moles per balloon are:

`n_(per\ balloon)=(1.00 atm*2.00L)/(0.082(atm*L)/(mol*K)*T)=24.39mol/T`

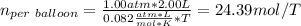
Then, the number of balloons are:

`balloons=(n_(transferred))/(n_(per\ balloon)) =(36402.5mol/T)/(24.39mol/T)\\ \\balloons=1492.5\ balloons`

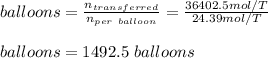
Which is more accurately 1493 balloons.

Regards.