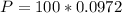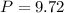Answer:
The value is
Step-by-step explanation:
From the question we are told that
The diameter is
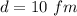
The position of the neutron of consider is between
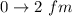
Generally the wave function representing the position of the neutron is mathematically represented as
![\Phi (x) = \sqrt{ (2)/(d) } sin [(\pi x)/(d) ]](https://img.qammunity.org/2021/formulas/physics/college/dzn37ovx80e3ten4zjnyvkjcua1et29ywb.png)
Generally probability that a neutron in the ground state is less than 2.0 fm from the edge of the nucleus (with the assumption that the diameter of both nucleus and neutron are symmetrical )is mathematically represented as
![=2 * \int\limits^2_0 { |\sqrt{ (2)/(d) } sin [(\pi x)/(d) ]|^2} \, dx](https://img.qammunity.org/2021/formulas/physics/college/qrm5czfmbd6azfclvx8mlczwkyjk935yq9.png)
![= (4)/(d) \int\limits^2_0 sin [(\pi x)/(d) ] \, dx](https://img.qammunity.org/2021/formulas/physics/college/hg1ietkdmjyh4u4i1j332olwjqv71yypqr.png)
From Trigonometry identity
![[sin(\theta)]^2 = (1- cos (2\theta ))/(2)](https://img.qammunity.org/2021/formulas/physics/college/31fmuuptrm7mpsngiq1bhjg3h74canmr1x.png)
So
![= (4)/(d) \int\limits^2_0 (1 - cos [(2\pi x)/(d) ])/(2) \, dx](https://img.qammunity.org/2021/formulas/physics/college/t7s9pvau75g4u5pl4xj1p62igzysqret31.png)
![=(2)/(d) [x - (sin [(2\pix)/(y) ])/([(2\pi)/(d) ]) ]\ |\left 2} \atop {0}} \right.](https://img.qammunity.org/2021/formulas/physics/college/ysoq8l9dn5j1nxiz57ks06snp7zt48m2wj.png)
![= (2)/(d) [2 - (sin[(2\pi (2))/(d) ])/((2\pi)/(d) ) ]](https://img.qammunity.org/2021/formulas/physics/college/mfss3exp46i1jdfq7vmlczq2oi5l5m39b8.png)
![= (2)/(10) [2 - (sin[(2\pi (2))/(10) ])/((2\pi)/(d) ) ]](https://img.qammunity.org/2021/formulas/physics/college/3zyzi170o6kdp2hh7syknyc5ql8gxgafs5.png)

Converting to percentage