Question

CAN SOMEONE PLEASE HELP ME WITH MY MATH ASAP PLEASE!!!​

Answer 1

The answer is :
`y =√(190)`

so, type 190 in the box

Explanation:

Notice that there are three right angle triangles in the image given. In order to create equations associated with the Pythagorean Theorem for the three triangles, we add the letters x and z to identify two sides that are missing information. Please see attached image for reference.

In the small right angle triangle on the right, the Pythagorean theorem tells us:

`x^2+10^2=y^2\\so\\x^2=y^2-100`

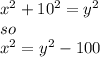
In the larger triangle :

`y^2+z^2=19^2\\z^2=361-y^2`

In the small triangle on the left:

`9^2+x^2=z^2`

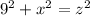
and in this last equation we can substitute the z-squared and the x-squared by the expressions we got before in the other two equations:

`9^2+(y^2-100)=(361-y^2)\\81+y^2-100= 361-y^2\\2\,y^2=361+100-81\\2\,y^2=380\\y^2=190\\`

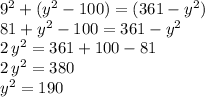
Then to solve for "y" we apply the square root:

`y =√(190)`