Answer:
Option C.
Explanation:
It is given that a histogram from 0 to 35 by 5’s. age (years). Beginning at 0 up to but not including 5, height of bar at each interval is 10, 8, 6, 3, 5, 3, 4.
The frequency table is:
Class interval frequency table Cumulative frequency
0-5 10 10
5-10 8 18
10-15 6 24 Median class
15-20 3 27
20-25 5 32
25-30 3 35
30-35 4 39
Sum of frequencies is 39, which is an odd number.
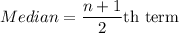
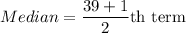
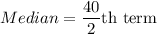
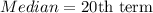
Now, we need a class whose cumulative frequency is more than 20 but its previous cumulative frequency is less than 20.
Median class is 10-15 because cumulative frequency of class 10-15 is 24. So 20th term is in the class 10-15.
Therefore, the correct option is C.