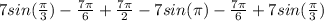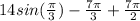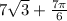Answer:
7√3 + 7π/6 ≈ 15.790
Explanation:
First, find the intersection:
7 cos(2x) = 7 − 7 cos(2x)
14 cos(2x) = 7
cos(2x) = 1/2
2x = π/3
x = π/6
From the graph:
On 0 ≤ x ≤ π/6, 7 cos(2x) > 7 − 7 cos(2x).
On π/6 ≤ x ≤ π/2, 7 − 7 cos(2x) > 7 cos(2x).
So the integral is:
![\int\limits^(\pi)/(6) _0 {[7cos(2x)-(7-7cos(2x))]} \, dx + \int\limits^(\pi)/(2) _(\pi)/(6) {[(7-7cos(2x))-7cos(2x)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/mhpy979ltf57q0fh06h5hm18zmntxu9k7w.png)
![\int\limits^(\pi)/(6) _0 {[7cos(2x)-7+7cos(2x))]} \, dx + \int\limits^(\pi)/(2) _(\pi)/(6) {[7-7cos(2x)-7cos(2x)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/z3arfqxlimz2qe56uuti785tkljehrwfdk.png)
![\int\limits^(\pi)/(6) _0 {[14cos(2x)-7]} \, dx + \int\limits^(\pi)/(2) _(\pi)/(6) {[7-14cos(2x)]} \, dx](https://img.qammunity.org/2021/formulas/mathematics/college/2c7ls0fp88nqpcp93neg8rhnxo4cmtrckr.png)
![[7sin(2x)-7x]|^(\pi)/(6) _0 + [7x-7sin(2x)]|^(\pi)/(2) _(\pi)/(6)](https://img.qammunity.org/2021/formulas/mathematics/college/yoayueh359zezma9y82p53x2kiy9hof1dl.png)
![[7sin((\pi )/(3) )-(7\pi )/(6) ] - [7sin(0)-0 ] + [(7\pi )/(2) -7sin(\pi )] - [(7\pi )/(6) -7sin((\pi )/(3) )]](https://img.qammunity.org/2021/formulas/mathematics/college/s6jg2nn8uhup6m6uxwutnow6ib36xcyz1a.png)