Question

Find the exact values of the six trigonometric functions of the angle.

1395°
sin 1395°
cos 1395°
tan 1395°

Answer 1

`\sin(1395)=-(\sqrt 2)/(2)\\\cos(1395)=(\sqrt 2)/(2)\\\tan(1395)=-1`

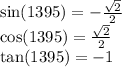
Explanation:

First, instead of doing 1395, let's find its coterminal angles. We can do so by subtracting 360 until we reach a solvable range. So:

`1395-360=1035`

This is still too high, continue to subtract:

`1035-360=675\\675-360=315\\315-360=-45`

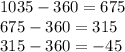
So, instead of 1395, we can use just -45.

So, evaluate each trig function for -45:

1)

`\sin(1395)=\sin(-45)`

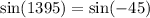
Remember that we can move the negative inside of the sine outside. So:

`=-\sin(45)`

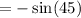
Remember the sine of 45 from the unit circle:

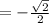
`=-(\sqrt2)/(2)`

2)

`\cos(1395)=\cos(-45)`

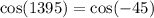
Remember that we can ignore the negative inside of a cosine function. So:

`=\cos(45)`

Evaluate using the unit circle:

`=(\sqrt 2)/(2)`

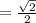
Now, remember that tangent is sine over cosine. So: "

`\tan(1395)=\tan(-45)=(\sin(-45))/(\cos(-45))`

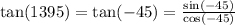
We already know them. Substitute:

`=(-(\sqrt 2)/(2))/((\sqrt 2)/(2))`

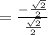
Simplify:

`=-1`

And we're done!