Question

The graph of a linear function cuts off an isosceles right triangle with legs 5 from the second quadrant of the coordinate plane. Find the linear function.

Answer 1

`f(x)=x+5`.

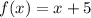Explanation:

It is given that the graph of a linear function cuts off an isosceles right triangle with legs 5 from the second quadrant of the coordinate plane as shown in below figure.

So, the linear function passes through the points A(-5,0) and B(0,5).

The equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`y-0=(5-0)/(0-(-5))(x-(-5))`

`y=(5)/(5)(x+5)`

`y=1(x+5)`

`y=x+5`

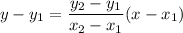
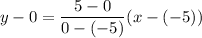
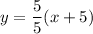
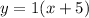
The linear function is

`f(x)=x+5`

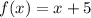
Therefore, the required linear function is
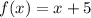`f(x)=x+5`.