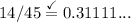Question

Convert the following repeating decimal to a fraction in simplest form .31 with the 1 repeating

Answer 1

14/45

Explanation:

So we have the fraction:

`0.3\bar1=0.31111...`

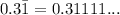
We can do this algebraically. Follow to following steps:

Let's let this number equal to n. Thus:

`0.31111...=n`

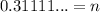
Since there is only 1 digit repeating, let's multiply everything by 10. So:

`3.1111...=10n`

Now, subtract n from both sides:

`3.1111-n=10n-n`

On the left, substitute the number for n. On the right, combine like terms:

`3.1111...-0.31111...=9n`

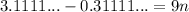
All of the 1s will cancel. So:

`3.1-0.3=9n`

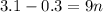
Subtract:

`2.8=9n`

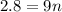
Divide both sides by 9:

`n=2.8/9`

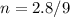
Remove the decimal by multiplying both sides by 10:

`n=28/90`

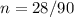
Reduce:

`n=14/45`

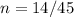
And we're done!

Use a calculator to check:

`14/45\stackrel{\checkmark}{=}0.31111...`