Answer:
Option (2).
Explanation:
Coordinates of points A(-2, 2), B(-1, -1), C(-1, 4) and (0, -2)
By using formula to get the length of any segment having extreme ends at
 and
and
 ,
,
d =
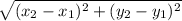
Length of segment AB =
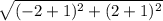
=
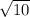 ≈ 3.16
≈ 3.16
Length of segment CD =
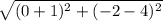
=
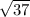 ≈ 6.08
≈ 6.08
Length of CD ≈ 2(length of AB)
But length of horizontal segments are equal.
Therefore, function 'f' is vertically stretched to form 'g'.
g(x) = 2f(x)
Now 'f' is translated by 1 unit right,
g(x) = 2f(x - 1)
Option (2) will be the answer.