Question

1/2 (5-2h) = h/2, solve for h

Answer 1

h = 1 2/3

Explanation:

1/2 (5-2h) = h/2

Multiply each side by 2

(5-2h) = h

Add 2h to each side

(5-2h +2h) = h+2h

5 = 3h

Divide by 3

5/3 = 3h/3

5/3 =h

1 2/3 = h

Check

1/2 (5-2*5/3) = 5/3/2

1/2 ( 5 - 10/3) = 5/6

1/2 ( 15/3 - 10/3) = 5/6

1/2 ( 5/3) = 5/6

5/6 = 5/6

Answer 2

A

Explanation:

So we have the equation:

`(1)/(2)(5-2h)=(h)/(2)`

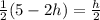
First, let's multiply both sides by 2 to get rid of the fractions. The 2s will cancel. So:

`2((1)/(2)(5-2h))=2((h)/(2))`

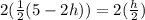
Simplify:

`5-2h=h`

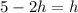
Add 2h to both sides:

`5=3h`

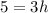
Divide both sides by 3:

`h=5/3`

Change into mixed fractions:

`h=1(2)/(3)`

So, our answer is A.

And we're done!

To check, substitute 5/3 back in:

`(1)/(2)(5-2(5/3))=((5/3))/(2)`

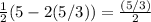
Multiply and divide:

`(1)/(2)(5-10/3)=(5)/(6)`

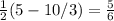
Subtract on the left:

`(1)/(2)(5/3)=(5)/(6)`

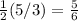
Multiply:

`(5)/(6)\stackrel{\checkmark}{=}(5)/(6)`

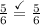
So, our answer is correct!