Question

2. A simple of 900 students has mean 3.5 cm and standard deviation 2.61 cm is the sample from a large population of mean 3.25 cm and standard deviation 2.61 cm? Check at 99% level of confidence. Also find the range. ​

Answer 1

The sample mean is not from a large population with mean 3.25 cm and standard deviation 2.61 cm

The range is
`3.28 < \mu <3.72`

Explanation:

From the question we are told that

The sample size is n = 900

The sample mean is
`\= x = 3.5 \ cm`

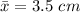
The standard deviation is
`s = 2.61 \ cm`

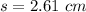
The population mean is
`\mu = 3.25 \ cm`

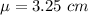
The population standard deviation
`\sigma = 2.61 \ cm`

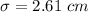
Given that confidence level is 99% the significance level is evaluated as

`\alpha = (100 - 99)\%`

`\alpha = 0.01`

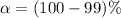
The critical value of
`(\alpha )/(2)` is obtained from the normal distribution table , the value is

`Z_{(\alpha )/(2) } = 2.58`

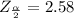
The null hypothesis
`\mu = \= x`

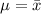
The alternative
`\mu \\e \= x`

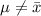
Generally the test statistics is mathematically represented

`t = (\= x - \mu )/( (s)/( √(n) ) )`

=>
`t = (3.5 - 3.25)/( (2.61)/( √(900) ) )`

=>
`t = 2.9`

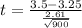
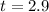
The p-value is from the z-table , the value is

`p-value = 2 P(Z > 2.61) = 2 * 0.0018658 = 0.004`

So we can see that
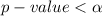`p-value < \alpha` so we reject the null hypothesis

Hence the sample mean is not from a large population with mean 3.25 cm and standard deviation 2.61 cm

Generally the margin of error is mathematically represented as

`E = Z_{(\alpha )/(2) } * (s)/(√(n) )`

`E = 2.58 * (2.61)/(√(900) )`

`E = 0.224`

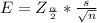
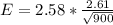
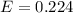
The range is evaluated as

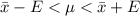
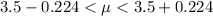
`\= x - E < \mu < \= x + E`

=>
`3.5 - 0.224 < \mu < 3.5 + 0.224`

=>
`3.28 < \mu <3.72`