Question

How do you do this question?

Answer 1

Explanation:

∫₁² [e^(1/x⁴) / x⁵] dx

∫₁² [e^(x⁻⁴) x⁻⁵] dx

If u = x⁻⁴, then du = -4x⁻⁵ dx, and -¼ du = x⁻⁵ dx.

∫ e^u (-¼ du)

-¼ ∫ e^u du

-¼ e^u + C

-¼ e^(x⁻⁴) + C

Evaluate between x=1 and x=2.

-¼ e^(2⁻⁴) − -¼ e^(1⁻⁴)

-¼ e^(1/16) + ¼ e

(e − ¹⁶√e) / 4

Answer 2

`=\frac{e-\sqrt[16]{e}}{4}`

Explanation:

So we have the definite integral:

`\int\limits^2_1{\frac{e^{(1)/(x^4)}}{x^5} \, dx`

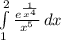
Again, we can use u-substitution. Let u equal 1/x^4. So:

`u=(1)/(x^4)=x^(-4)`

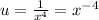
Find the derivative:

`du=-4x^(-5)=-4((1)/(x^5))dx`

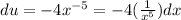
Divide by -4. So du is:

`-(1)/(4)du=(1)/(x^5)dx`

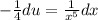
Of course, we also need to change our bounds. Substitute 1 and 2 into u:

`u=1/(2)^4=1/16\\u=1/(1)^4=1/1=1`

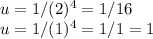
Therefore, our new bounds are from 1 to 1/16.

So, make the substitutions:

`=-(1)/(4)\int\limits^(1)/(16)_1 {e^u} \, du`

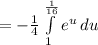
The integral of e^u is just e^u. So:

`=-(1)/(4)(e^u)`

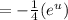
Evaluate for the bounds:

`=-(1)/(4)(e^{(1)/(16)}-e^(1))`

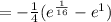
Simplify:

`=-\frac{\sqrt[16]{e}-e}{4}`

Distribute:

`=\frac{e-\sqrt[16]{e}}{4}`

And we're done!