Question

A proton starting from rest travels through a potential of 644 X 106V and then moves into a uniform magnetic field, B = 0.02 T, perpendicular to the protons velocity. What is the radius of the proton's resulting orbit in m? Mp 1.67 x 10-27 kg, e = 1.6 x 10-19 C.

Answer 1

Given :

Potential ,

`P=644 * 10^6\ V\\ \\P=6.44* 10^8\ V`

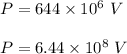
Uniform magnetic field , B = 0.02 T .

Mass of proton ,
`M_p=1.67* 10^(-27)\ kg` .

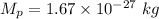Charge on proton ,
`e=1.6* 10^(-19)\ C` .

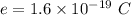Also , velocity of proton is perpendicular to magnetic field .

To Find :

The radius of the proton's resulting orbit .

Solution :

Now , when velocity is perpendicular to magnetic field radius of orbit is given by :

`r=\sqrt{(2VM_p)/(eB^2)}`

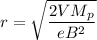
Putting all given values above :

`r=\sqrt{(2* 6.44* 10^8* 1.67* 10^(-27))/(1.6* 10^(-19)* 0.02^2)}\\\\r=183.33 \ m`

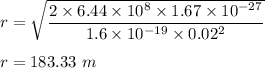
Therefore , radius of orbit is 183.33 m .

Hence , this is the required solution .