Question

1.A steel cable is attached to a ring on the top of a street light. The weight of the street light is W . The other end of the cable is attached to the side of a tall building. The street light is pulled to one side by a horizontal chain and held stationary above the road. Fig. 1.1 shows the cable at 55° to the vertical. The tension in the cable is 43.6 N. a) A force of size W is produced by adding the tension in the horizontal chain and the tension in the cable as vectors. i) State the direction of the vector sum of these two forces. ii) In the space below, draw to scale a vector diagram to determine . State the scale used. Scale used: …………………………… W = ……………………………. iii) Calculate the mass of the street light. mass = …………………. kg

Answer 1

a) Please find attached, the vector diagram regarding the question

i) The direction of the sum of the vectors is the negative direction of the vertical or y-axis

ii) The scale is 1 mm = 1 N

W = 25 N

The mass of W is approximately 2.55 kg

Step-by-step explanation:

The given parameters are;

The angle of inclination of the cable to the vertical = 55°

The tension in the cable = 43.6 N

a) i) The direction of the vector sum of the two forces is given as the resultant of the two forces;

The component of the tension in the chain is given as follows;

Tension in the horizontal chain = x
`\mathbf{ \hat i}`

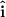
The resolved force in the cable is given as follows;

Given that the force is acting upwards along the cable

F = 43.6 × -sin(55°)
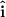`\mathbf{ \hat i}` + 43.6 × cos(55°)
`\mathbf{ \hat j}`

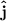
F ≈ -35.72
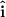`\mathbf{ \hat i}`+ 25
`\mathbf{ \hat j}`

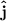
Therefore, from ∑Fₓ = 0 and ∑F
`_y` = 0, since the horizontal force in the chain will balance the horizontal component of the tension in the cable, there will be no net horizontal force and the resultant force will have a direction of the vertical y-axis

ii)

Given that ∑F = 0, we have;

The tension in the cable is an horizontal force, therefore, we have;

∑Fₓ = 0

The tension in the horizontal chain + The horizontal component of the cable = 0

The tension in the horizontal chain - 35.72 N = 0

∴ The tension in the horizontal chain = 35.72 N

The weight of the street light + The vertical component of the tension = 0

The weight of the street light + 25 N = 0

Therefore;

The weight of the street light W = -25 N

The scale of the vector diagram used is 1 mm = 1 N

W = -25 N

The mass of the street light = Weight of the street light/(Acceleration due to gravity)

The mass of the street light = 25 N/(9.81 m/s²) ≈ 2.55 kg