Question

I just need no. a please help me to prove this. ​

Answer 1

Answer: see proof below

Explanation:

Given: A + B + C = π and cos A = cos B · cos C

scratchwork:

A + B + C = π

A = π - (B + C)

cos A = cos [π - (B + C)] Apply cos

= - cos (B + C) Simplify

= -(cos B · cos C - sin B · sin C) Sum Identity

= sin B · sin C - cos B · cos C Simplify

cos B · cos C = sin B · sin C - cos B · cos C Substitution

2cos B · cos C = sin B · sin C Addition

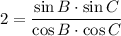`2=(\sin B\cdot \sin C)/(\cos B \cdot \cos C)` Division

2 = tan B · tan C

`\text{Use the Sum Identity:}\quad \tan(B+C)=(\tan B+\tan C)/(1-\tan B\cdot \tan C)`

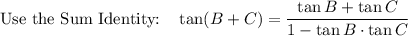
Proof LHS → RHS

Given: A + B + C = π

Subtraction: A = π - (B + C)

Apply tan: tan A = tan(π - (B + C))

Simplify: = - tan (B + C)

`\text{Sum Identity:}\qquad \qquad \qquad =-\bigg((\tan B+\tan C)/(1-\tan B\cdot \tan C)\bigg)`

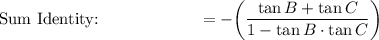
Substitution: = -(tan B + tan C)/(1 - 2)

Simplify: = -(tan B + tan C)/-1

= tan B + tan C

LHS = RHS: tan B + tan C = tan B + tan C
`\checkmark`