Unfortunately your teacher is using x as both a variable and a multiplication sign. This is something that can be avoided by using something like the asterisk symbol to indicate multiplication.
Anyways, notice how the expression
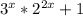 shows up twice. Once in the numerator (the entire numerator) and once again in the denominator (nearly the whole thing)
shows up twice. Once in the numerator (the entire numerator) and once again in the denominator (nearly the whole thing)
Let's replace that messy expression with the variable y. So we're letting

This means,
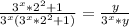
At this point you can probably see how to get
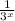 from here. The y terms cancel out when we divide leaving 1 up top and 3^x down below.
from here. The y terms cancel out when we divide leaving 1 up top and 3^x down below.