Question

31. Tan 15° + Tan 30° + Tan 15° Tan 30º = ?​

Answer 1

The expression equals 1 (one)

Explanation:

Recall that all these trigonometric values have exact expression in forms of square roots.

There is also a very important rule for the tangent of an addition of angles, which states:

`tan(\alpha +\beta)=(tan(\alpha)+tan(\beta))/(1-tan(\alpha)\,tan(\beta))`

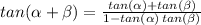
We can use this with
`\alpha=15^o\,\,\,\,and\,\,\,\beta=30^o`

`tan(15^o +30^o)=(tan(15^o)+tan(30^o))/(1-tan(15^o)\,tan(30^o))`

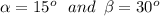
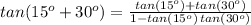
since tan of 15 degrees plus 30 degrees is tangent of 45 degrees, which we know is exactly 1 (one), we can multiply both sides of the equal sign by the denominator on the right, and then solve for exactly the expression we want to find:

`tan(45^o)=(tan(15^o)+tan(30^o))/(1-tan(15^o)\,tan(30^o))\\1=(tan(15^o)+tan(30^o))/(1-tan(15^o)\,tan(30^o))\\1-tan(15^o)\,tan(30^o)=tan(15^o)+tan(30^o)\\1=tan(15^o)\,tan(30^o)+tan(15^o)+tan(30^o)\\tan(15^o)+tan(30^o)+tan(15^o)\,tan(30^o)=1`

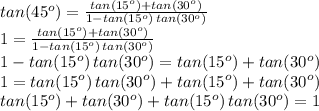
So the answer we are looking for is 1 (one)