Question

At Elisa's printing company, there are two kinds of printing presses: Model A, which can print 70 books/ day, and model B, which can print 55 books per day. The company owns 14 total printing presses that allow them to print 905 books per day. How many model A presses do they have?

Answer 1

9 Model As.

Explanation:

Let A represent Press A and let B represent Press B.

So, they own 14 total presses. This means that:

`A+B=14`

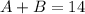
They can print 905 books per day, in other words, since A prints 70 per day and B prints 55 per day:

`70A+55B=905`

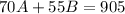
This is now a system of equations. Solve by substitution. From the first equation, subtract B from both sides:

`A=14-B`

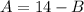
Substitute this into the second equation: "

`70(14-B)+55B=905`

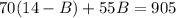
First, we can divide everything by 5 to simplify things:

`14(14-B)+11B=181`

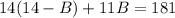
Distribute the left:

`196-14B+11B=181`

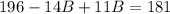
Combine like terms:

`-3B+196=181`

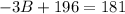
Subtract 196 from both sides:

`-3B=-15`

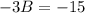
Divide both sides by -3

`B=5`

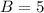
So, the company has 5 Model B presses.

Which means that the company has 14-5 or 9 Model A presses.

And we're done!