Question

Select all the transformations of f(x) = x2 that combine to result in the graph of function g below.

A parabola with vertex negative 1 comma negative 2 that opens downward. The graph passes through the points negative 3 comma negative 3 and 1 comma negative 3.

Group of answer choices

vertical stretch by a factor of 2

translation of 1 unit right

translation of 2 units up

translation of 1 unit left

reflection across the x-axis

horizontal stretch by a factor of 2

translation of 2 units down

Answer 1

The transformations of
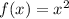`f(x) = x^2` Translation of 1 unit left, reflection across the x-axis, and translation of 2 units down. So, Options D, E and G is correct choice.

Let's break down the transformations applied to
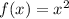`f(x) = x^2` to obtain the graph of function:

A parabola with a vertex at (-1, -2) that opens downward: This implies a reflection across the x-axis and a translation of 1 unit left and 2 units down.

Passes through (-3, -3) and (1, -3): Both points lie on the line y=−3, so this is a translation of 3 units down.

Now let's compare these transformations to the given choices:

A. Vertical stretch by a factor of 2: This isn't part of the transformations.

B. Translation of 1 unit right: The transformation involved a 1 unit left translation.

C. Translation of 2 units up: The transformation involved a 2 units down translation.

D. Translation of 1 unit left: Correct

E. Reflection across the x-axis: Correct

F. Horizontal stretch by a factor of 2: This isn't part of the transformations.

G. Translation of 2 units down: Correct

Therefore, the correct transformations are:

D. Translation of 1 unit left

E. Reflection across the x-axis

G. Translation of 2 units down

Answer 2

Options 4, 5 and 7.

Explanation:

The general function is

`f(x)=x^2`

The vertex form of a parabola,

`g(x)=a(x-h)^2+k` ...(1)

where, a is a constant and (h,k) is vertex.

It is given that vertex of a parabola is (-1,-2).

`g(x)=a(x-(-1))^2+(-2)`

`g(x)=a(x+1)^2-2` ...(2)

It passes through (-3,-3).

`-3=a(-3+1)^2-2`

`-3+2=4a`

`-1=4a`

`-(1)/(4)=a`

Put this value in (2).

`g(x)=-(1)/(4)(x+1)^2-2`

Now,

h=1>0, so translation of 1 unit left.

a=-1/4<0 Reflection across the x-axis and vertical compression by factor 4.

k=-2<0, translation of 2 units down

Therefore, the correct options are 4, 5 and 7.