Question

If f(x) and its inverse function, f Superscript negative 1 Baseline (x), are both plotted on the same coordinate plane, where is their point of intersection?

Answer 1

(2,2)

Step-by-step explanation:

The point of their intersection is

Line that go near through the points

(0,6) and

(3,0)

Determine the slope

`m = (0-6)/(3-0)`

= -2

The function f(x) while intercept the slope is equivalent to

f(x) = -2x + 6

Now replace tha variable for x to y and y to x

Now we will assume y = f(x)

So, y = -2y + 6

Now Isolate the variable y

2y = -x + 6

y = -0.5x + 3

Assume

`f^(-1) (x) = y\\\\f^(-1) (x) = -0.5x + 3`

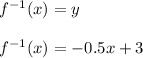
Now we will solve the equations

`f(x) = -2x + 6\\\\f^(-1)(x) = -0.5x + 6`

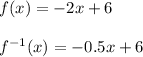
Now equate these two equations like as below

-0.5x + 3 = -2x + 6

now we will solve the value of x

2x - 0.5x = 6 - 3

1.5x = 3

x = 2

Now put the value of x in any of the equations

f(x) = -2(2) + 6 = 2

The solution is the point (2,2)

Hence,

Their point of intersection is (2,2)