Question

A right-angled triangle has shorter side lengths exactly 2 cm and

3 cm respectively. Find the exact length of the hypotenuse​

Answer 1

√13

Explanation:

2²+3²=c²

4+9=c²

13=c²

c=√13

Answer 2

3.60555128 cm or √13 cm

Explanation:

Since this is a right triangle, we can use the Pythagorean Theorem.

`a^2+b^2=c^2`

where
`a` and
`b` are the legs and
`c` is the hypotenuse.

We know the shorter legs are 2 cm and 3 cm. We don't know the hypotenuse.

`a=2\\b=3`

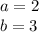
Substitute the values into the formula.

`2^2+3^2=c^2`

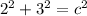
Evaluate the exponents.

⇒2²=2*2=4

`4+3^2=c^2`

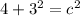
⇒3²=3*3=9

`4+9=c^2`

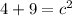
Add 4 and 9.

`13=c^2`

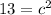
c is being squared. The inverse of a square is the square root. Take the square root of both sides of the equation.

`√(13) =√(c^2)`

`√(13)=c`

`3.60555128=c`

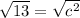
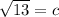
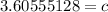
Add units, in this case centimeters, or cm.

`c=3.60555128 cm`

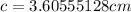
The length of the hypotenuse is 3.60555128 or √13 centimeters.