Answer:
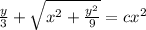
Explanation:
I initially got stuck at the very beginning because I did the product rule wrong T-T
Isolate the y' by dividing out the x in front of it and simplify a bit. Then substitute y/x for a variable (I chose z), replace all applicable variables, and simplify where needed.
At this point it should be separable! Separate the variables as you normally would and integrate to solve.
- For the x portion you could probably, technically leave the +c as is and work with from there. But turning the c into ln(c) [which is fair because the constant is arbitrary] helps us simplify it to be used later on.
- For the z integral, use a trig. substitution for tangent and reduce to get the integral of secant. Remember that you have to swap the variables back from theta into z because the integral is indefinite!
Lastly, use the previous z=y/x relationship to replace the z portions and get your answer in terms of the original x and y variables.
My work is in the attachment. Comment woth questions or if something seems off.