Question

Rewrite in simplest rational exponent form x^1/2*X^1/4

Answer 1

x ^ (3/4)

Explanation:

x^1/2*X^1/4

When we multiply and the bases are the same we can add the exponents

x ^ ( 1/2 + 1/4)

x ^ ( 2/4 + 1/4)

x ^ (3/4)

Answer 2

`\sqrt[4]{x^3}`

Explanation:

First, let's examine our original statement.

`x^{(1)/(2) }\cdot x^{(1)/(4)}`

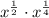
Using exponent rules, we know that if we have
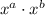`x^a \cdot x^b`, then simplified, the answer will be equivalent to
`x^(a+b)`.

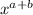So we can simplify this by adding the exponents
`(1)/(2)` and
`(1)/(4)`.

Converting
`(1)/(2)` into fourths gets us
`(2)/(4)`.

`(2)/(4) + (1)/(4) = (3)/(4)`.

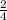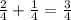So we now have
`x^{(3)/(4)}`.

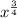When we have a number to a fraction power, it's the same thing as taking the denominator root of the base to the numerator power.

Basically, this becomes

`\sqrt[4]{x^3}`. (The numerator is what we raise x to the power of, the denominator is the root we take of that).

Hope this helped!