Answer:
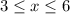
Explanation:
So we want to find the domain of:
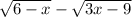
Recall that the radicands cannot be negative. In other words, they must be greater than or equal to 0. So, to solve the domain, determine the restrictions of each radical:
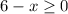
Add x to both sides:
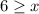
Flip:

So, for the first radical, x must be less than or equal to 6.
Second radical:
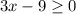
Add 9 to both sides:
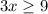
Divide both sides by 3:

So, our domain is:
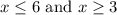
Therefore, as a compound inequality, this is:
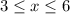
This is our domain.
And we're done!