Answer:
5115
Explanation:
First of all, we need to assume there is a typo involved, and that the expression is supposed to be ...
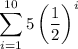
The values being summed look a lot like the general term of a geometric sequence:
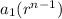
The exponents in the sum range from 1 to 10, so the values being summed range from 5/2 to 5/1024. In order for that to be the case with our general term, for r = 1/2, we must have a1 = 5/2 as we let n range from 1 to 10.
The sum of the terms of the geometric sequence is ...
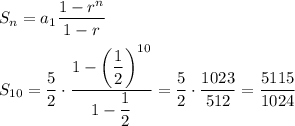
The numerator of the fraction is ...
x = 5115
_____
Caveat
If we have misinterpreted the intent of the problem statement, the answer will be different.