Question

11. Mr Lee bought a second hand car for

$25 480 and made a down payment of
$10 000. He arranged to pay the balance at
the end of two years with compound interest
at 4.75%. How much did he pay at the
stipulated time?

Answer 1

Depends on the rate compound interest is accrued. See answers.

Explanation:

We need the compound interest formula which is:

`A = P (1+(r)/(n) )^(nt)`

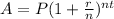
A = final amount

P = initial principal balance

r = interest rate

n = number of times interest applied per time period

t = number of time periods elapsed

It doesn't say how frequently the interest is compounded, so we will do monthly, quarterly, and yearly.

MONTHLY

So we know the car costs $25,480 and he made a down payment of $10,000. By subtracting the down payment from the purchase price we find the loan amount.

$25,480 - $10,000 = $15,480

P = 15,480

r = 4.75% = .0475

n = 12 (12 months in a year)

t = 2

Plug everything into the compound interest formula.

`A = P (1+(r)/(n) )^(nt)`

`A = 15480(1+(.0475)/(12))^(12*2)`

`A = 15480(1+(.0475)/(12))^(24)`

`A = 15480(1+.00396)^(24)`

`A = 15480(1.00396)^(24)`

`A = 15480*1.0992`

`A = $17016.14`

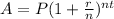
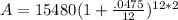
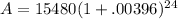
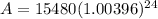
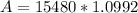
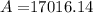
Mr. Lee paid $17,016.14 when the bill came due at 2 years with interest compounded monthly.

QUARTERLY

P = 15,480

r = 4.75% = .0475

n = 4 (4 quarters in a year)

t = 2

`A = P (1+(r)/(n) )^(nt)`

`A = 15480(1+(.0475)/(4))^(4*2)`

`A = 15480(1+(.0475)/(4))^(8)`

`A = 15480(1+.0119})^(8)`

`A = 15480(1.0119)^(8)`

`A = 15480*1.099`

`A = 15480(1.099)`

`A = 17013.20`

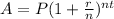
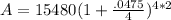
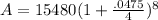
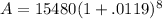
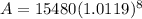
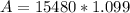
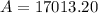
Mr. Lee paid $17,013.20 when the bill came due at 2 years with interest compounded quarterly.

YEARLY

P = 15,480

r = 4.75% = .0475

n = 1

t = 2

`A = P (1+(r)/(n) )^(nt)`

`A = 15480(1+(.0475)/(1))^(1*2)`

`A = 15480(1+(.0475)/(12))^(2)`

`A = 15480(1+.0475})^(2)`

`A = 15480(1.0475)^(2)`

`A = 15480*1.0973`

`A = 16985.53`

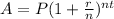
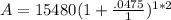
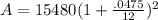
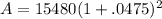
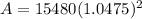
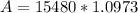
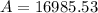
Mr. Lee paid $16,985.53 when the bill came due at 2 years with interest compounded yearly.