Question

Use quadrilateral ABCD to find the value of x. The figure is not drawn to scale. Use the following dimensions: m⦨ABC = 4x◦, m⦨BCD = 3x◦, m⦨CDA = 2x◦, m⦨DAB = 3x◦. Use the formula, (n – 2)180 to find the total degrees of the polygon. Write an equation and solve for x. You found the measures of the 4 interior angles in Question 2. Now, explain in 2-3 sentences how you can use them⦨CDA to find the measure of exterior angle ⦨ADE. Find them⦨ADE

Answer 1

Answer/Step-by-step explanation:

Question 1:

Interior angles of quadrilateral ABCD are given as: m<ABC = 4x, m<BCD = 3x, m<CDA = 2x, m<DAB = 3x.

Since sum of the interior angles = (n - 2)180, therefore:

`4x + 3x + 2x + 3x = (n - 2)180`

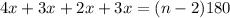
n = 4, i.e. number of sides/interior angles.

Equation for finding x would be:

`4x + 3x + 2x + 3x = (4 - 2)180`

`12x = (2)180`

`12x = 360`

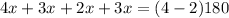
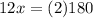
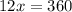
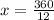`x = (360)/(12)` (dividing each side by 12)

`x = 30`

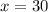
Find the measures of the 4 interior angles by substituting the value of x = 30:

m<ABC = 4x

m<ABC = 4*30 = 120°

m<BCD = 3x

m<BCD = 3*30 = 90°

m<CDA = 2x

m<CDA = 2*30 = 60°

m<DAB = 3x

m<DAB = 3*30 = 90°

Question 2:

<CDA and <ADE are supplementary (angles on a straight line).

The sum of m<CDA and m<ADE equal 180°. To find m<ADE, subtract m<CDA from 180°.

m<ADE = 180° - m<CDA

m<ADE = 180° - 60° = 120°