Question

A plane takes off and travels at an angle of 50° north of east at 90 mph for 3 hours. It then adjusts its path to head 30° west of north and travels in that direction for an hour at a speed of 100 mph. Approximately how far away is the plane from its starting point?

Answer 1

271 miles

Explanation:

Answer 2

303.8 miles.

Explanation:

Using the given information, draw a figure as shown below.

90 mph for 3 hours = 270 miles

100 mph of 1 hour = 100 miles

In triangle ABC,

`\angle ABC=50^(\circ)+50^(\circ)=100^(\circ)`

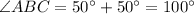
Using cosine formula,

`AC^2=AB^2+BC^2-2(AB)(BC)\cos B`

`AC^2=(270)^2+(100)^2-2(270)(100)\cos (100^(\circ))`

`AC^2=72900+10000-54000\cdot\left(-0.174\right)`

`AC^2=92296`

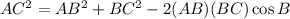
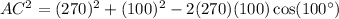
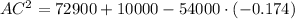
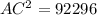
Taking square root on both sides.

`AC=√(92296)`

`AC\approx 303.8`

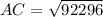
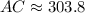
Therefore, the plane is 303.8 miles from its starting point.