Answer:
Relative to Sir George's starting point, the knights collide at a distance of 38.43 m from Sir George's starting point.
Step-by-step explanation:
Let the distance covered by Sir George be
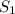
and the distance covered by Sir Alfred be

Since the knights collide, hence they must have traveled for the same amount of time just before collision
From one of the equations of motion for linear motion

Where
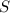 is the distance traveled
is the distance traveled
 is the initial velocity
is the initial velocity
 is the acceleration
is the acceleration
and
 is the time
is the time
For Sir George,

 = 0 m/s (Since they start from rest)
= 0 m/s (Since they start from rest)
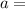 0.21 m/s²
0.21 m/s²
Hence,
 becomes
becomes
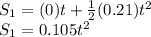
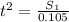
Now, for Sir Alfred

 = 0 m/s (Since they start from rest)
= 0 m/s (Since they start from rest)
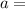 0.26 m/s²
0.26 m/s²
Hence,
 becomes
becomes
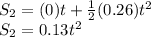
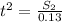
Since, they traveled for the same time,
 just before collision, we can write
just before collision, we can write
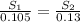
Since, the two nights are 86 m apart, that is, the sum of the distances covered by the knights just before collision is 86 m. Then we can write that
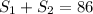 m
m
Then,
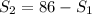
Then,
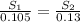 becomes
becomes
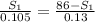
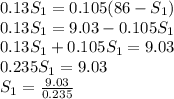
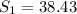 m
m
∴ Sir George covered a distance of 38.43 m just before collision.
Hence, relative to Sir George's starting point, the knights collide at a distance of 38.43 m from Sir George's starting point.