Question

Calculate, correct to one decimal place, the acute angle between the lines 3x - 4y + 5 = 0 and 2x + 3y - 1= 0.

Answer 1

70.6°

Explanation:

The angle between the 2 lines can be calculated using

tanΘ = |
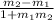`(m_(2)-m_(1) )/(1+m_(1)m_(2) )` | ( Θ is the angle between the lines )

The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

Rearrange the 2 equations into this form to extract the slopes

3x - 4y + 5 = 0 ( subtract 3x + 5 from both sides )

- 4y = - 3x - 5 ( divide all terms by - 4 )

y =
`(3)/(4)` x +
`(5)/(4)` with m =
`(3)/(4)` ←
`m_(2)`

--------------------------------------------

2x + 3y - 1 = 0 ( subtract 2x - 1 from both sides )

3y = - 2x + 1 ( divide all terms by 3 )

y = -
`(2)/(3)` x +
`(1)/(3)` with m = -
`(2)/(3)` ←
`m_(1)`

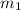
Note it does not matter which slope is labelled
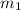`m_(1)` or
`m_(2)`

Thus

tan Θ = |
`((3)/(4)+(2)/(3) )/(1+(-(2)/(3))(3)/(4) )`

= |
`((17)/(12) )/((1)/(2) )` = |
`(17)/(6)` | =
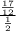`(17)/(6)` , then

Θ =
`tan^(-1)` (
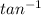`(17)/(6)` ) ≈ 70.6° ( to 1 dec. place )