Question

: The interior wall of a furnace is maintained at a temperature of 900 0C. The wall is 60 cm thick, 1 m wide, 1.5 m broad of material whose thermal conductivity is 0.4 W/m K. The temperature of the outside surface of the wall is 150 0C. Determine the heat through the wall. Also determine thermal resistance to heat flow.

Answer 1

Heat is lost at the rate of 750 J/s or W

The thermal resistance is 1 K/W

Step-by-step explanation:

interior temperature
`T_(2)` = 900 °C

wall thickness t = 60 cm = 0.6 m

width = 1 m

breadth = 1.5 m

thermal conductivity k = 0.4 W/m-K

outside temperature
`T_(1)` = 150 °C

heat through the wall = ?

The area of the wall A = w x b = 1 x 1.5 = 1.5 m^2

Temperature difference
`dt` =
`T_(2)` -
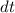`T_(1)` = 900 - 150 = 750 °C

note that
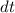`dt` is also equal to 750 K since to convert from °C to K we'll have to add 273 to both temperature, which will still cancel out when we subtract the two temperatures.

To get the heat that escapes through the wall, we use the equation

Q = Ak
`(dt)/(t)`

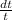
substituting values, we have

Q = 1.5 x 0.4 x
`(750)/(0.6)` = 750 J/s or W

Thermal resistance
`R_(t)` =
`(dt)/(Q)`

`R_(t)` = 750/750 = 1 K/W