Question

The interior of a regular polygon is 5 times the exterior angle

I. Find the interior angle of the polygon
II. Find the exterior angle of the polygon
III. How sides has the polygon
IV. What is the name of the polygon​

Answer 1

Explanation:

The interior angle of a polygon is given by

`((n - 2) * 180)/(n)`

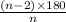
The exterior angle of a polygon is given by

`(360)/(n)`

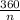
where n is the number of sides of the polygon

The statement

The interior of a regular polygon is 5 times the exterior angle is written as

`((n - 2) * 180)/(n) = 5( (360)/(n) )`

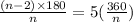
Solve the equation

That's

`(180n - 360)/(n) = (1800)/(n)`

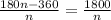
Since the denominators are the same we can equate the numerators

That's

180n - 360 = 1800

180n = 1800 + 360

180n = 2160

Divide both sides by 180

n = 12

I).

The interior angle of the polygon is

`((12 - 2) * 180)/(12) = (10 * 180)/(12) \\ = (1800)/(12)`

The answer is

150°

II.

Interior angle + exterior angle = 180

From the question

Interior angle = 150°

So the exterior angle is

Exterior angle = 180 - 150

We have the answer as

30°

III.

The polygon has 12 sides

IV.

The name of the polygon is

Dodecagon

Hope this helps you.