Question

Filiate
Consider the line MU for M(-1, 1) and U(4, 5).
what’s the distance from M to U ?

Answer 1

`\boxed{ \bold{ \huge{ \boxed{ \sf{ √(41) \: \: units}}}}}`

Explanation:

Let M ( -1 , 1 ) be ( x₁ , y₁ ) and U ( 4 , 5 ) be ( x₂ , y₂ )

Finding the distance from M to U

`\boxed{ \sf{distance = \sqrt{ {(x2 - x1)}^(2) + {(y2 - y1)}^(2) } }}`

`\longrightarrow{ \sf{ \sqrt{ {(4 - ( - 1))}^(2) + {(5 - 1)}^(2) } }}`

`\longrightarrow{ \sf{ \sqrt{ {(4 + 1)}^(2) + {(5 - 1)}^(2) } }}`

`\longrightarrow{ \sf{ \sqrt{ {(5)}^(2) + {(4)}^(2) } }}`

`\longrightarrow{ \sf{ √(25 + 16)}}`

`\longrightarrow{ \sf{ √(41) }}` units

The distance from M to U is
`\sf{ √(41) \: \: units}`

Hope I helped!

Best regards! :D

Answer 2

The answer is

`√(41) \: \: or \: \: 6.403 \: \: \: units`

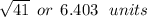
Explanation:

The distance between two points can be found by using the formula

`d = \sqrt{ ({x1 - x2})^(2) + ({y1 - y2})^(2) } \\`

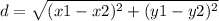
where

(x1 , y1) and (x2 , y2) are the points

From the question the points are

M(-1, 1) and U(4, 5)

The distance from M to U is

`|MU| = \sqrt{ ({ - 1 - 4})^(2) + ( {1 - 5})^(2) } \\ = \sqrt{ ({ - 5})^(2) + ( { - 4})^(2) } \\ = √(25 + 16)`

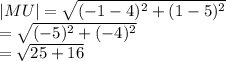
We have the final answer as

`√(41) \: \: or \: \: 6.403 \: \: \: units`

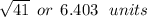
Hope this helps you