Answer:
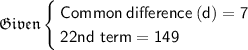
We've to find out the sum of 20 terms. So, n = 22
By using nth term Formula of the AP :
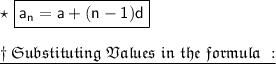
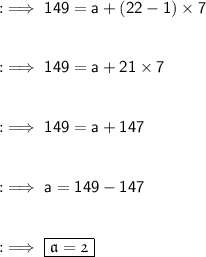

______________________
For any Arithmetic Progression ( AP ), the sum of n terms is Given by :
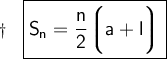
Where :
- a = First Term
- n = no. of terms
- l = Last Term
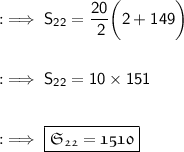

⠀⠀⠀━━━━━━━━━━━━━━━━━━━━━⠀
⠀