Question

Find the resultant of the following forces by component method: F1 =12N,south; F2 =24N, 30° north of west; F3 = 15N, 75° south of west; and F4 = 32 N, 50° south of east.​

Answer 1

The resultant of given forces is
`\vec R = -16.099\,\hat{i} -27.002\,\hat{j}\,\,[N]`.

Step-by-step explanation:

The component method consists in summing each component of known vectors in rectangular form to get the resultant. That is:

`\vec R = \left(\Sigma_(i=1)^(m) x_(i)\right)\,\hat{i}+\left(\Sigma_(i=1)^(m) y_(i)\right)\,\hat{j}`

Where:

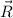`\vec R` - Resultant, measured in newtons.

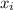`x_(i)` - i-th x-Component, measured in newtons.

`y_(i)` - i-th y-Component, measured in newtons.

We describe each known vector below:

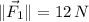`\|\vec F_(1)\| = 12\,N`, South:

`\vec F_(1) = -12\,\hat{i}\,\,[N]`

`\|\vec F_(2)\| = 24\,N`,
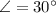`\angle = 30^(\circ)` North of west:

`\vec F_(2) = 24\cdot (-\cos 30^(\circ)\,\hat{i}+\sin 30^(\circ)\,\hat{j})\,[N]`

`\vec F_(2) = -20.785\,\hat{i}+12\,\hat{j}\,\,[N]`

`\|\vec F_(3)\| = 15\,N`,
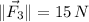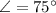`\angle = 75^(\circ)` South of west:

`\vec F_(3) = 15\cdot (-\cos 75^(\circ)\,\hat{i}-\sin 75^(\circ)\,\hat{j})\,\,[N]`

`\vec F_(3) = -3.883\,\hat{i}-14.489\,\hat{j}\,\,[N]`

`\|\vec F_(4)\| = 32\,N`,
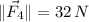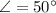`\angle = 50^(\circ)` South of east:

`\vec F_(4) = 32\cdot (\cos 50^(\circ)\,\hat{i}-\sin 50^(\circ)\,\hat{j})\,\,[N]`

`\vec F_(4) = 20.569\,\hat{i} -24.513\,\hat{j}\,\,[N]`

We find the resultant by vectorial sum:

`\vec R = \vec F_(1)+\vec F_(2)+\vec F_(3)+\vec F_(4)`

`\vec R = (-12-20.785-3.883+20.569)\,\hat{i}+(12-14.489-24.513)\,\hat{j}\,\,[N]`

`\vec R = -16.099\,\hat{i} -27.002\,\hat{j}\,\,[N]`

The resultant of given forces is
`\vec R = -16.099\,\hat{i} -27.002\,\hat{j}\,\,[N]`.